Statistical Arbitrage
Statistical Arbitrage Strategy relies on the historically strong correlation between two financial instruments, for example, WTI and Brent, DE30 and F40, Amazon and Apple. Users can set a period for correlation determination, timeframe, and strong correlation level. The software sells strong and buys weak instruments when their correlation diverges beyond a certain level. Once mean reversion occurs, the locked position created by the two orders: buy and sell, should generally be in profit. This strategy is also known as convergence or pair trading.
THE CORE PRINCIPLE
Statistical arbitrage relies on mean reversion principles and the law of large numbers. The underlying belief is that the relative prices of financial instruments that are historically correlated will revert to their mean over time. This is where statistical arbitrage occurs – it capitalizes on price discrepancies between these correlated instruments when they deviate from their historical norm.
For instance, consider two stocks that have moved together historically. If their prices diverge – one increases in price, and the other decreases – a statistical arbitrageur would sell short the outperforming stock and buy the underperforming one, betting that the “spread” between the two would eventually converge.
SPREAD – TO THE PRICE DIFFERENCE OR DISCREPANCY BETWEEN TWO RELATED FINANCIAL INSTRUMENTS.
In statistical arbitrage, the term ‘spread’ typically refers to the price difference or discrepancy between two related financial instruments. These could be two different stocks, futures contracts, forex pairs, or even cryptocurrency tokens.
For example, one might track the spread between two historically co-integrated stocks in a pair trading strategy (a common form of statistical arbitrage). When the spread, or the difference in their prices, deviates significantly from its historical mean (average), it signals an opportunity to trade.
Suppose the spread widens too much, indicating one stock is overpriced and the other is underpriced relative to their historical relationship. In that case, a trader may sell short the overpriced stock and buy the underpriced one. Conversely, if the spread narrows excessively, they would do the opposite.
The spread is expected to be mean-reverting in statistical arbitrage, meaning it fluctuates around a long-term average value. Traders expect that when the spread deviates significantly from this mean, it will eventually return to it, allowing them to profit from this reversion.
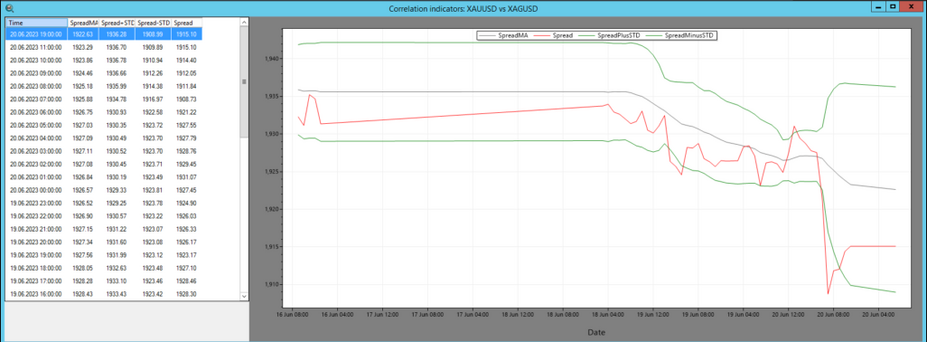
In the SharpTrader platform Spread Indicator is used to visualize the correlation between two assets. The calculation of the correlation involves the following components:
- Spread: This refers to the numerical difference or distance between the values of two assets.
- SpreadMA: It represents the moving average of the spread over a specific period, determined by pi_SpreadMA_Period.
- STD (Standard Deviation): It calculates the classic standard deviation of the spread relative to SpreadMA. The number of observations used is equal to pi_SpreadMA_Period.
To trigger the opening of trades, the software follows the principles of statistical arbitrage theory.

STATISTICAL ARBITRAGE – CORRELATION MATRIX
A correlation table, also known as a correlation matrix, is a table that shows the correlation coefficients between many variables. Each cell in the table shows the correlation between two variables. The value is in the range of -1 to 1.
If two variables have a correlation of 1, they move in the same direction, i.e., when one increases, the other increases, and vice versa. This is known as a perfect positive correlation.
If two variables correlate -1, they move in opposite directions, i.e., when one variable increases, the other decreases, and vice versa. This is known as a perfect negative correlation. A correlation of 0 means that no relationship exists between the variables.
Here’s a simple example of a correlation table for three variables: A, B, and C:
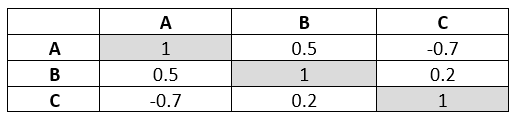
In this table, the correlation between variables A and B is 0.5 (a moderate positive correlation), while the correlation between A and C is -0.7 (a strong negative correlation). The diagonal of the matrix from the top left to the bottom right is always 1 because a variable is perfectly correlated with itself.
These tables are widely used in various fields, including finance, where they help in determining the relationship between different financial variables or the returns of different assets, useful for portfolio diversification and risk management.
Statistical strategy instruments and order tab
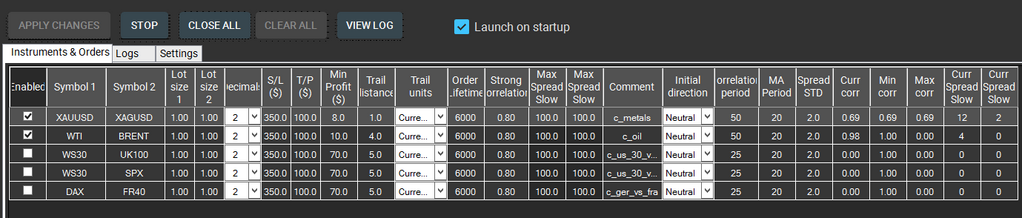
Description of the parameters:
Enabled – enables or disables trading on a selected instrument.
Symbol 1 – symbol name on side 1
Symbol 2 – symbol name on side 2.
Lot size 1 – lot size to be traded on side 1.
Lot size 2 – lot size to be traded on side 2.
Decimals – number of decimal places in symbol quotes.
S/L – hidden stoploss for an arbitrage trade, expressed in currency.
T/P – hidden takeprofit for an arbitrage trade, expressed in currency.
Min profit – starting point for trailing, expressed in currency.
Trail distance – distance arbitrage trade is trailed at.
Trail units – allows to switch trailing units between currency and percents.
Order lifetime – maximum arbitrage deal duration (expressed in seconds)
Strong correlation
Max Spread Slow 1 – maximum allowed spread on side 1. If actual spread is higher than Max spread slow value, arbitrage signals are ignored.
Max Spread Slow 2 – maximum allowed spread side 2. If actual spread is higher than Max spread fast value, arbitrage signals are ignored.
Comment – internal order identifier. If several instances of the same instrument are used in the strategy, comments for each instance should be different.
Initial direction – allows to set initial directions for lock orders. If selected 'Buy on 1' or 'Sell on 1' it will open trades only by signals in allowed directions. 'Neutral' allows to open trades in any direction.
Correlation period - number of bars for correlation calculation
MA period - moving average period
Spread STD - standard deviation. The standard deviation is always positive or zero. The standard deviation is small when the data are all concentrated close to the mean, exhibiting little variation or spread. The standard deviation is larger when the data values are more spread out from the mean, exhibiting more variation.
Curr corr -current correlation between 2 instruments
Min corr- minimal correlation between instruments that was detected during software was running
Max corr- maximal correlation between instruments that was detected during software was running
Curr Spread Slow 1 – current spread for instrument 1
Curr Spread Slow 2 – current spread for instrument 2